In this presentation, we will take a look at how to calculate simple interest a few different ways. As we look at this, you may ask yourself, why are we going over this a few different ways, why not just go over it one way, the best way. And let us learn that well and be able to apply it in each situation. While one way does work in most situations. In other words, we will probably learn one way have a favorite way to calculate the simple interest and apply that in every circumstance. It’s also the case that when we look at other people’s calculations or technical calculation, they may have some different form of the calculation. For example, I prefer away when I think about the calculation of simple interest to have some subtotals in the calculation and have more of a vertical type of calculation the way we would see if done in something like a calculator. If we see a type of equation in a book, then the idea there is that Have the most simple type of equation expressed in as short a way as possible. And that typically is going to be some type of formula. And that formula will often not be showing the subtotal.
01:12
So in other words, a textbook has an incentive to show a very compressed type of format for calculating something. And individuals, if we want to go back for Intuit, note what happened in it, then we often will benefit by having some subtotals in the calculations that we work through. That’s one type of difference we want to know. Other reason we want to know different methods is just to understand the math a bit better if we understand different approaches, we understand what we are actually doing a little bit better. Another reason is that different people are going to have different minds in terms of how they think of things and how they process things. So we want to be able to look at someone else’s work and say, Okay, I see what they did here and be able to apply that to ourselves and see what they’re doing. And again, The more we can understand how other people process things, the better we understand what the material is, and how to communicate it to other people. So let’s go through a few of these types of ways we can calculate simple interest.
02:12
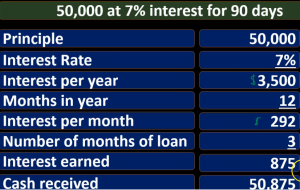
So we’re going to start with a loan of 50,007% interest rate, and it’s a 90 day loan, it’s gonna be out for 90 days. So we’ll start out with the loan amount 50,000. For our first calculation type, we’re going to multiply that times 7%. Now note, if we have a calculator, we’re typically going to do that by saying 50 50,000 50,000 times point O seven, point O seven if we’re an Excel, we format these Excel to be percents. We can have a percent we can use this percent button up here, but I typically use decimal point oh seven if we move the decimal two places to the right, then of course, we would have a 7% and that would give us the 3500. So in other words, 50,000 times 7% is 3,501st thing we need to note, this 7% means 7% a year, unless expressed otherwise, whenever we say that something is so much percent, typically we mean percent a year. So for example, if we say we have a mortgage, we pay the mortgage monthly, but we typically express the month the mortgage rate as a yearly rate.
03:21
Why would we do that? You know, there’s a couple different reasons we might do that. But one main reason that it’s a convention for us to do that is if we took point O seven, and said we want a monthly type of interest rate, if we divide that by 12, we get a pretty small number. So it would be point five, eight, something something percent, which is pretty small, we don’t really, that’s that’s a range, it’s more difficult for us to express in. Therefore we typically express interest rates for that reason, and just it’s a convention in years. So unless expressed otherwise, just note within a problem with any type of discussion, interest typically means a year and it’s similar to before We’re talking about salary. Like we say someone makes 70,000, we typically probably mean 70,000 a year, even if not stated, then we’re going to take that amount, and we’re going to say how many days are in a year. Now in this calculation, we’re taking 360 to make an even rather than 365, which is an assumption of 12 months, times 30 days in a month. Of course, there are 31 days or 30 days or 28 days or 29 days in a month.
04:29
But if we do a nice even calculation here, we get an even 360 for our simple interest calculation. So that’s what we will use at this time. So then we’re going to take the 3500 per year of interest. This is the dollar amount, and this is going to be 360 days, gives us about $10 a day. Again, that’s rounded, it’s really 3500 divided by 360 gives us 9.6. them in tu tu tu tu. So I’m going to use this 10 here just to show it. That’s how you’ll see it in Excel if you take the decimals off, but note that we’re really going to be multiplying by that nine, something. Just remember, when you deal with interest, you have to deal with that not everything’s going to run out to the dollar, not everything’s gonna run out to the penny will have some rounding differences. So then we’re going to take that times 90 that number times 90 days, and that’ll give us 875. Again, not 90 times 10, in this case, because we’re using that rounded numbers as we would see in something like an Excel worksheet. So you just got to kind of deal with those kinds of things. So if it was 10 times 90, it would be 900. What we really have is the 360 divided by 3500. Let’s do that one more time what we really have this 3500 divided by 360 or 9.72, which was rounded to 10 Taking off the pennies. And then we take that, and we multiply it times 90 days.
06:06
Now that gives us our 875. So then if we take our 875, that’s how much we would earn, then for the time period for the 90 days at 7%, for simple interest, if we take the original amount of the loan 50,000 we loaned out at the one, we add to it the 875, then we get 50,008 75, that we would then receive at the end of the long term. This is the way that one of the ways I think is the most easy to see this. And that’s if we break it out by days, depends on the loan type if we want to break it out by days or months. So if it’s less than, if it’s less than a year, then it might be that we want to use days if it problems giving very specific, then we’ll have to use the actual, you know, number of days in the month just got to be careful on the terms of the problem. If it’s going to be a longer term problem, then we might just round these two months and use months as the calculation as well. See this time, same type of idea, we’ll take the 50,000, multiply times 7%, that’s going to give us our 3500 50,000 times 7%. The yearly rate gives us the 3500 interest per year. Now we’re going to take that and we’re going to instead of dividing it by 360 days, we’ll divide it by 12, giving us the interest rate per month 3500 divided by 12. So again, if we did that with the calculator, we’re taking three five divided by 12. neck is not exactly nine to 92, but 290 1.6666 on forever.
07:40
Note that even if I put the pennies there, it’s not always going to be exact, and we’re just have to deal with that. That’s going to be some rounding issues. We will always have when we when we do these types of calculations. Then we’re going to take that amount and multiply it times three. Where do we get three, three months, 90 days divided by Are convention 30 days per month about gives us three months, then we’re going to take the this dollar amount per month times the number of months three, give us that 875. Remember, we’re not talking about the 9292, necessarily, we’ll have rounding there to off by $1. because really what we’re talking about is the 3500 divided by 12, or 290 1.6666, on forever, times three, and that’ll give us our 875. So just be careful of the rounding, it’s always gonna be a problem doesn’t matter how many places we take it out to someone, the decimals will repeat forever. So we’ll have the 50,000 plus the 875, getting us to that same 50,008 75.
08:48
These two ways the prior weight by day in this way by month are the easiest way for me to think about it, because it’s linear. This is how you plug it into a calculator. This shows us each step and the subtotal. However, if you were to represent it with with it shorter away as possible, then these subtotals aren’t something that are typically going to be represented in textbooks, because it’s not as neat, not as nice. So when you put things out and you calculate them, I would remember them in this format. This is easier for me to remember than a shorter type of formula. Because the shorter formula doesn’t make intuitive sense. I can’t say we’ll walk through this and say, Well, this is the yearly interest rate, this is the rate per year. And then we’re going to take the rate per per month, times the number of months to get the interest. So I can’t really tell the story to myself. The longer story that I can tell is easier for me to remember. Then a shorter formula which has no story that makes any sense. So anyways, bottom line, I would remember one of these two methods, and four, your default method.
09:58
Okay, so now we’re going to do an Other methods, we’re going to start off with the number of days in the loan 90, we’re going to divide that by the number of days in the year. This, of course, is called a ratio. So we’re comparing and starting off with the comparison of the loan term, 90 days, divided by the number of days in the year 360, which again, is 12 times 30. For our purposes, rounding it, center 365, it’s 360. And that’s going to give us point two, five or 25%. So here’s our ratio given us point two, five. Now that we have that ratio, we can take that ratio at point two five and multiply it times the interest per year, which was that 3500 or 50,000 times point oh seven, that 3500 and that will give us our 875. So note, this gets at 875. A bit faster here we don’t have as many calculations or as many steps. However, I find that most students and myself included are Think about this, the ratio doesn’t make as intuitive sense to me as saying, oh, here’s the interest rate per year, here’s what the interest would be per year, and then breaking out to either a daily or monthly interest rate and then multiply it times the number of months, same math, same end result, just a different order of calculations.
11:19
So just be aware that this because it’s smaller, probably often more represented in a textbook or something, we need to be able to see that. So then we got the 875. Plus the 50,000 original gives us the loan that we’ll get back at the end of this time period. If we loaned out 50,000 at 7%, simple interest, 90 days, we should get back 50,008 75. Next, we’ll do the same type of thing. But now we’re going to do this by the number of months and alone. So remember, this is going to be 90 divided by 30 gives us three months in the loan. And then we’re going to take that and compare it to 12 three divided by 12 three over 12 Fact gives us the ratio of three to 12. So three divided by 12 will give us that same 25. So note we’re doing the same thing. Of course, because we’re doing the comparison of the timeframe, the loan is over over the total timeframe. And as long as we use the same measuring tools, ones, we’re in this case using months, or in the prior case, we use dates for both the loan term and the amount of time within the year, we will get to the same ratio, point two, five is the percent. So then we’re going to, of course, you can simplify these down to and see that the same ratio three, three over 12.
12:40
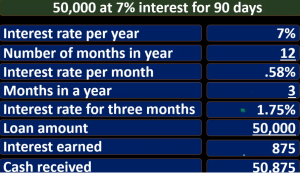
If you simplify that down, then and you simplify the 30 compared to or the 90 compared to the 360, you’ll get to the same ratios, right. So there’s the point two, five, and then we’re going to take that multiply times at 3500, which once again is of course, the $50,000 loan. We started with times point four times point oh seven point post seven 3500. And that’ll give us the 870 5.25 times 3500 gets us back to that 875. So once again, it’s quicker method than the first two, we started off with a little less intuitive, in my experience with myself and people I’ve worked with, for most people understand, I believe total cash received in would be this 50,008 75. Next method. Now we’re going to try to break this percentage out as we saw at the beginning and break it out into a monthly rate. And we’ll deal with that. So we’re going to say we’re going to start with the interest rate this time and say that’s the yearly rate. That’s what default by default typically is divided by 12.
13:50
And that will give us the monthly rate. So once again, if I did this when a calculator would say, point oh seven, that’s the 7% divided by the number of months in a year. Well, gives us point oh 58333 on forever, that’s a pretty small number, which once again is the reason we don’t typically do that. We don’t typically represent the interest rate in terms of months. Because it typically is a small number, and it’s just not the convention that we just have out of whatever reason we come up with conventions for. So that’s what we’re gonna have if we break it down to a monthly rate. Now, it’s important to know this because when you put stuff into Excel, or other types of financial couch calculators at times, then it sometimes uses this monthly rate. So we’ll need to know the rate per period. And that’s in this case, the monthly rate. And so it’s important for us to know this type of calculation when we use tools such as Excel, so that’ll give us point 258 percent remember that it’s not exact here, this is a rounding times the loan of 50,000 gives us 292 So once again, be careful of the rounding all the time.
15:04
Because this is point 598, you might first think it’s 58%, it’s not, we got to move the decimal two places to the left, which was point 0058 is what it really represents times 50,000. But even that’s a couple bucks off. Why? Because this is rounded too. So remember what we had it’s point O seven divided by 12 gives us point 00583333. And that’s what we’re using times 50,000. So again, just be careful, I could give an example that is perfectly even here or, but it’s not, I’d rather given a less than perfect example to show that it’s not going to be perfect. All the time. It’ll be perfect sometimes. So this would be the amount of interest per month simple interest per month. And now we just need to say that’s $1 sign by the way. Now they’re gonna say there’s how many months in the We’re going to say that in the term of the loan three, or 90 divided by 33 months, so 292 times three would be 875. Once again, that might be a bit of rounding there. If we say 292 times eight times three, we’re going to get 876.
16:21
Why? Because really, what we had remember is point O seven divided by 12, which is point O five, eight. And then we multiply that times the 50,000. To get really, to nine 1.6666 divided our times three, that’s going to be our 875. And then if we take the 875 plus the 50,000 gives us that same 50,008 75. One more time, one more way, and then we’ll stop this. Okay, so we’re gonna take that same interest 7% Break it down to a monthly rate. So 7% divided by 12 gives us at point eight 7.58%. Once again, this is rounded, same spot we were at last time, we now have a monthly percent percent. Now we’re going to take that and multiply times the number of months. So we have 50, we have 90 days divided by three divided by 30 gives us three months.
17:26
So if we take that point five, eight rounded, this is rounded times the three, we get about 1.75. And this thing would be the interest rate per the time period we’re talking about three months or 90 days. So in other words, we take a look at this we have the interest rates point, oh seven for a year, divided by 12 gives us the interest rate per month. If I move the decimal point over it’s point five, eight Three, three, this is rounded, this isn’t 58%. Remember, point five, eight a difference. And then we’re going to take that times the number of months three. And that’s going to give us point 0175 or 1.75%. So this is actually exact now 1.75%. And then we’re going to take that times the loan amount, 50,000. And that’ll give us the 875. So remember this, what we did here is we broke down the percent for a three month time period, or 90 days. And again, that’s not usual. We don’t usually say that we don’t usually say, Hey, we’re going to pay you a simple interest rate of whatever for a three month time period.
18:41
So just you know, be aware that we don’t typically say that we’re going to pay you point five eight per month, we typically express things oftentimes with a yearly rate, that yearly rate often being between one in like 20, and therefore being at an interest rate that makes more sense to us. It’s weird. within that range, so but when we do financial calculations, this once again might be a way that we could see this within the the periods that we’re talking about, which in this case, is a 90 day or three month period. So then we just take that interest rate times the 50,000 gives us the 875. We add that to the original 50, we get to that same 50,008 75. So again, I hope this wasn’t too confusing or more confusing than it was helpful. But note that when you see these types of calculations in a textbook, they’re often so simplify, they look to be like the easiest way to see it, they are the easiest way to write it. But obviously, it’s oftentimes a longer type of calculation.
19:41
A more vertical calculation rather than a horizontal type of formula is easier for us to think through, tell a story in our head, remind yourself what we’re actually doing. In order to better memorize the calculation for future use an application to other types of problems, as well as to just have a format and be able to To understand it better for future use and know what we’re actually doing rather than spitting out a number that we think is correct just based on the formula, but not having any intuitive realization or understanding what it’s for and therefore how we can use it to apply to something